Sobre o site > Análise Multivariada > Componentes principais

Componentes Principais

# para exemplificar a utilização da análise de componentes principais ou principal component analysis (PCA), vamos considerar as médias das medidas de comprimento dos dígitos de 15 animais nelore, 15 curraleiros, 15 pantaneiros e 12 búfalos, contidas no quadro abaixo (dados parciais da dissertação de Silva 2012)

	A	B	C	D	E
Búfalo	0.34	0.72	0.61	0.63	5.39
Curraleiro	0.60	0.46	0.26	0.49	4.54
Nelore	0.86	0.64	0.33	0.53	4.95
Pantaneiro	0.59	0.52	0.30	0.53	4.56

# baixe os dados via web

dados<-read.table("https://19e31fa08e.cbaul-cdnwnd.com/fd58c287e8dcea635dc0088984f5a026/200000016-b6ee0b765f/digitos.txt",header=TRUE, sep="", dec=".")

# após entrar com a tabela acima em um objeto (data.frame) denominado de "dados", obtemos os componentes principais utilizando a função "prcomp"

cp=prcomp(~A+B+C+D+E, scale = TRUE, data=dados)

# a análise é gravada em um objeto aqui denominado "cp"

# na função deve-se acrescentar o nome das variáveis, o argumento scale (opcional mas recomendado) refere-se a padronização dos dados (TRUE=padroniza os dados) e o argumento data indica o nome do objeto onde estão contidas as variáveis

# a importância de cada variável para a variância obtida em cada componente é tanto maior quanto maior for o valor (em módulo) associado a variável

# observe abaixo que para o primeiro componente todas as variáveis contribuem para a variância e tem importância no estudo (apesar de pequena superioridade da variável C)

# para o segundo componente a variável de maior importância é a A


Standard deviations:
[1] 2.033349e+00 9.077014e-01 2.038829e-01 5.646475e-16

Rotation:
         PC1         PC2        PC3         PC4
A -0.3204996 -0.83524822  0.1099610  0.38065822
B  0.4454724 -0.46343394  0.2486452 -0.37843193
C  0.4899380  0.08733382 -0.1748664  0.80383126
D  0.4865881  0.05482483  0.6689900  0.03392931
E  0.4711975 -0.27741022 -0.6692969 -0.25415095

# pode-se também observar a importância de cada variável pela correlação entre a matriz de correlação dos dados com a matriz de componentes (chega-se a mesma conclusão acima)

cor(cor(dados), cp[[2]])

      PC1        PC2         PC3        PC4
A -0.9777456 -0.9264544  0.03186677  0.0943770
B  0.9885728  0.7328249 -0.10800235 -0.3879260
C  0.9997947  0.8378016 -0.08120713 -0.2516533
D  0.9996691  0.8367275 -0.05927786 -0.2586718
E  0.9961929  0.7762294 -0.12236727 -0.3297475

# uma outra informação importânte é o quanto da variância é acumulada com os dois primeiros componentes

summary(cp)

Importance of components:
                          PC1    PC2     PC3       PC4
Standard deviation     2.0333 0.9077 0.20388 5.646e-16
Proportion of Variance 0.8269 0.1648 0.00831 0.000e+00
Cumulative Proportion  0.8269 0.9917 1.00000 1.000e+00

# a variância acumulada deve ser de no mínimo de 70% para a análise ser considerada acurada, sendo que neste caso atinge 99%

# com o gráfico dos dois primeiros componentes pode-se avaliar a similaridade entre os grupos e as correlações entre as variáveis

biplot(cp)

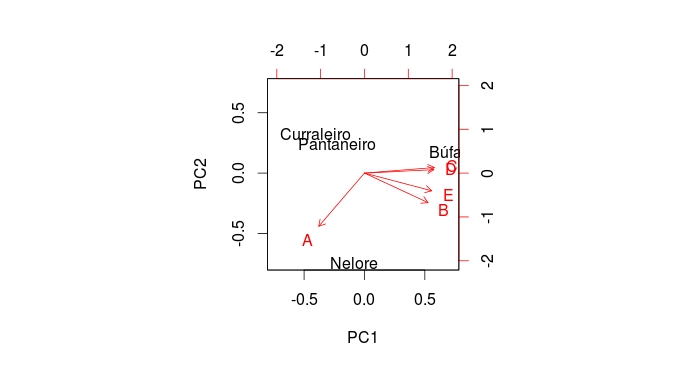
# fazendo alguns ajustes no gráfico

biplot(cp, xlim=c(-0.9,0.9), ylim=c(-0.8,0.8), ylab="Componente 2 (16%)", xlab="Componente 1 (83%)", col=1)

abline(h=0, v=0, lty=2, col=2)

points(x=0,y=0,pch=1,cex=30, col="dark blue")

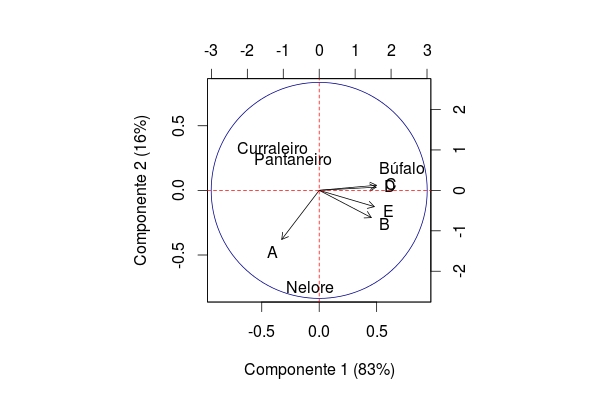
# observa-se que os curraleiros e os pantaneiros são mais similares (mais próximos no gráfico) e os nelores e búfalos mais distantes são menos similares

# as variáveis C e D são correlacionadas positivamente (com o angulo aproximando de zero a correlação aproxima de +1)

# as variávies A e B tem correlação próximo a zero (com angulo aproximando a 45 graus a correlação aproxima a 0)

# as variáveis A e C tem correlação negativa (quando angulo aproximando a 180 graus a correlação aproxima de -1)

# veja as correlações de pearson e compare com o gráfico de componentes principais

require(ds)

dscor(dados)

 pairs correlation p-value
1  A and B     -0.2702  0.7298
2  A and C     -0.7101  0.2899
3  A and D     -0.6795  0.3205
4  A and E     -0.4365  0.5635
5  B and C      0.8672  0.1328
6  B and D      0.8822  0.1178
7  B and E      0.9669  0.0331
8  C and D      0.9847  0.0153
9  C and E      0.9394  0.0606
10 D and E      0.9168  0.0832

# por fim pode-se obter gráficos com maior controle

c=cp$x

c=as.data.frame(c)

attach(c)

x1=c$PC1# primeiro componente

x2=c$PC2 # segundo componente

# obter o gráfico para observar a similaridade entre os grupos

plot(x2~x1, ylab= "Componente 2 (16%) ", xlab= "Componente 1 (83%) ", cex=0, xlim=c(-5,5), ylim=c(-3,3), bty="n", axes=FALSE)

axis(1,c(-4,-3,-2,-1,0,1,2,3,4))

axis(2,c(-4,-3,-2,-1,0,1,2,3,4))

text(x1,x2, label=rownames(dados), cex=1.2, col=c(rep(2),rep(3), rep(4),rep(5)))

abline(v=0,h=0, lty=2, col="dark blue")

rect(4,0.6,2,0, lty=2)

rect(-1.8,-1.8,1.1,-1, lty=1)

rect(-3,1,0.7,0, lty=3)

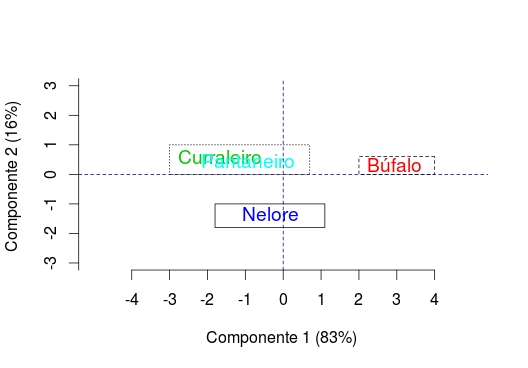
# gráfico para observar as correlações

cpr=as.data.frame(cp$rotation)

y1=cpr$PC1

y2=cpr$PC2

plot(y1,y2, cex=0, xlim=c(-0.4,0.6), xlab="PC1", ylab="PC2")

text(y1,y2, label=rownames(cpr), pos=4)

arrows(0,0,y1,y2, lty=2, col="dark blue")

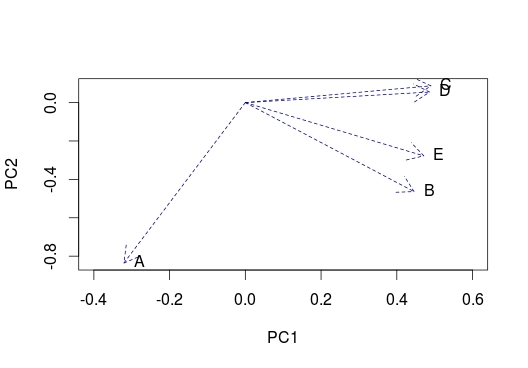
Referências

Silva, L.H. Morfometria radiográfica e tomográfica de dígitos de bovinos e bubalinos. Dissertação. Universidade Federal de Goiás. Curso de Pós Graduação em Ciência Animal. 63p.